Tree


  • Overview of Trees
  • Terminologies
  • Types of Trees
  • Tree Traversals
  • Traversals-Illustration
  • Binary Trees
  • Types of Binary Trees
  • Implementation in Python
  • Binary Tree Traversals
  • Implementation of Binary Trees
  • Applications of Binary trees
  • Binary Search Trees
  • Implementation Of BST

    • Practice Questions

    Tree Traversals

    Tree traversal:

    ·       Tree traversal means reading or processing the data of a node exactly once in some order in a tree.

    ·       Data structures like Arrays and Linked Lists have logical start and logical end but trees are not linear therefore they can be traversed in many different ways.

     

    Types of Tree traversal:

    1.       Breadth First Traversal (level order)

    2.       Depth First Traversal

    a.       Preorder Traversal

    b.       Inorder Traversal

    c.       Postorder Traversal

    Level Order Traversal:

    In this type of traversal, the tree nodes are traversed in a layer by layer pattern.

    Consider, below example:

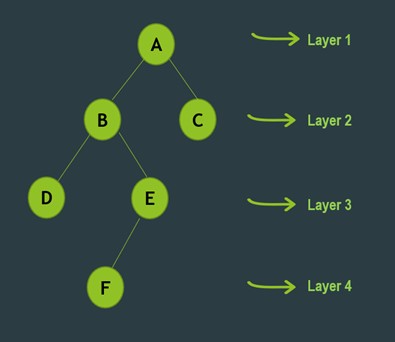
    In this example, in this tree the order of traversal is that we start from node A of Layer 1,

    then we traverse nodes B and C of Layer 2, then nodes D and E in Layer 3, and

    then finally node F of last Layer 4.

    So the final order of this traversal will look like this: A B C D E F

     

     

    Depth First Traversal types:

     

    1. Preorder Traversal

    First we traverse the root data, then the left-subtree and then the right-subtree.

    <Root> <Left> <Right>

    def traverse_Preorder(self, root):

                            if root is not None:                               

                                        print(root.data)

                                        self.traverse_Preorder(root.left)

                            self.traverse_Preorder(root.right)

     

     

    2. Inorder Traversal

    First we traverse the left-subtree, then the root data and then the right-subtree.

    <Left> <Root> <Right>

    def traverse_Inorder(self, root):

                            if root is not None:

                                        self.traverse_Inorder(root.left)

                                        print(root.data)

                                        self.traverse_Inorder(root.right)

     

    3. Postorder Traversal

    First we traverse the left subtree, then the right subtree and then the root data.

    <Left> <Right> <Root>

    def traverse_Postorder(self, root):

                            if root is not None:

                                        self.traverse_Postorder(root.left)

                            self.traverse_Postorder(root.right)

                            print(root.data)

     

     

     

    Try here>>>